Riešenie príkladu TSP - Analytické myslenie

Spoločne sa pozrieme na TSP príklad z roku 2018, ktorý sa objavil v analytickom subteste. Znalosť výrokov v ňom ale nebolo treba, stačilo aplikovať základné počty. (Pre ľahšie vyhľadávanie ide o TSP variantu 01, príklad 33)

Príklad TSP MUNI:

Bežecký závod na 6 km má na trati vyznačené body, ktorých vzdialenosť od štartu udáva nasledujúca tabuľka:

Kontrola 1 sa nachádza medzi pätinou a štvrtinou trasy, od kontroly 1 je potrebné zabehnúť tretinu dĺžky závodu ku kontrole 2. Kontrola 3 je v troch štvrtinách trasy a ku kontrole 4 je to z nej menej než šestinu dĺžky závodu. Z kontroly 4 zostáva už menej než osmina trasy do cieľa. Iné kontroly v závode nie sú. Vyberte nepravdivé tvrdenie:

1. Medzi vrcholom V a hotelom H sú dve kontroly.
2. Kontrola 2 je za vrcholom V.
3. Medzi rybníkom R a vrcholom V je jedna kontrola.
4. Medzi mostom M a cieľom C nie je žiadna kontrola.
5. Kontrola 4 je pred mostom M.

Pokúste sa zvyknúť si na to, aby ste sa najskôr pozreli na to, na čo máte odpovedať. V tomto prípade máme hľadať nepravdivé tvrdenie. To znamená, že si budeme musieť podľa indícií rozpísať všetko, čo zo zadania dokážeme zistiť a potom hodnotiť pravdivosť tvrdení jedného po druhom. Všetky tvrdenia sa týkajú informácie, kde sú umiestnené kontroly - skúsime si ich teda jednoduchými výpočtami rozmiestniť najpresnejšie, ako to len bude možné.

Zadávatelia nám poskytujú rozpis vzdialeností jednotlivých bodov od štartu v tabuľke. Myslíme si, že na tento druh úlohy by nám najlepšie poslúžila jednoduchá osa, do ktorej by sa nám jednoducho dopĺňali jednotlivé kontroly. Môžeme si tak v rýchlosti takúto osu vytvoriť, pričom vzdialenosti jednotlivých bodov od seba nie je potrebné graficky riešiť, kľudne body rozmiestnite rovnomerne a s číslami nám pomôže ich zadaná tabuľka.

Do osi si postupne zaznačte kontroly 1-4 podľa toho, čo sa vám o nich podarí zistiť.

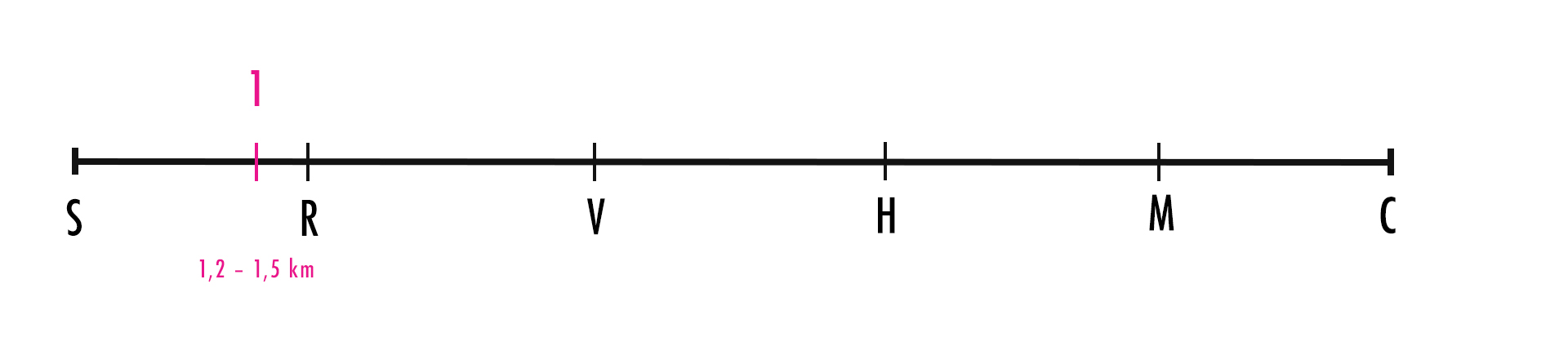
Kontrola 1

“Kontrola 1 sa nachádza medzi pätinou a štvrtinou trasy”

Vieme, že vzdialenosť SC, teda dĺžka celej trasy je 6 km. Musíme si teraz len vyrátať, čomu sa rovná pätina a štvrtina, čo nám dá potrebné rozmedzie pre bod 1.

1/5 z 6 = 1,2

1/4 z 6 = 1,5

(Ak vám tieto výpočty robia problém, pozrite sa na článok Koľko matematiky je potrebnej k TŠP?)

Čo sme zistili? Neprezradili nám to síce presne, ale to vôbec nevadí. Stačí nám vedieť, že kontrola 1 sa nachádza medzi 1,2 km a 1,5 km, a prvý bod na ose sa pritom nachádza až v 1,6 km. S istotou teda môžeme kontrolu 1 umiestniť pred bod R:

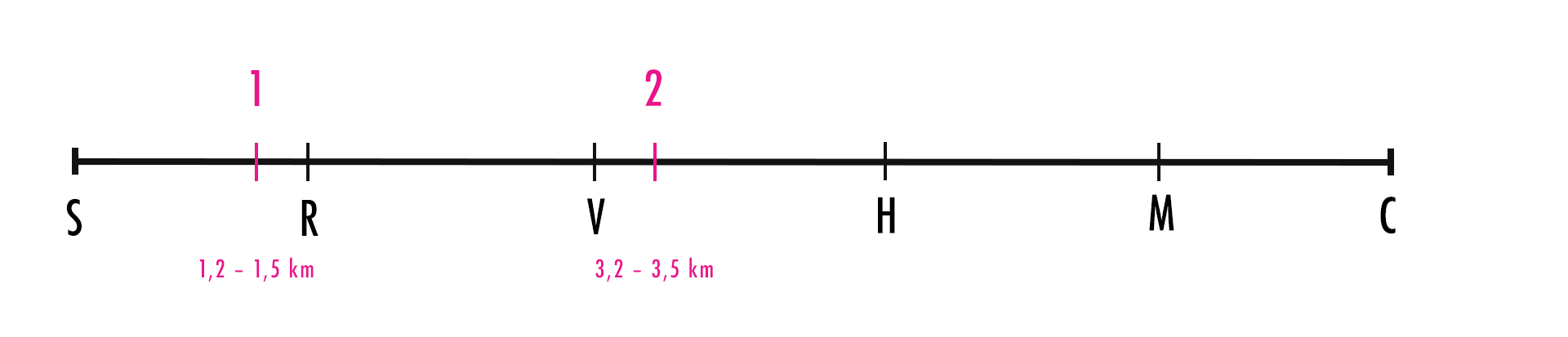
Kontrola 2:

“od kontroly 1 je potrebné zabehnúť tretinu dĺžky závodu ku kontrole 2”

Tretina dĺžky závodu, teda tretina z 6 km = 2 km. Vieme teda že kontrola 2 je presne o 2 km ďalej, ako kontrola 1. Dá nám teda rozmedzie 3,2 km - 3,5 km. Opäť nám pomôže aj toto nie úplne presné určenie bodov, pretože ak sa bod V nachádza na 3,1 km a bod H až na 4,8 km, vieme s istotou, že kontrola 2 sa nachádza medzi bodmi V a H:

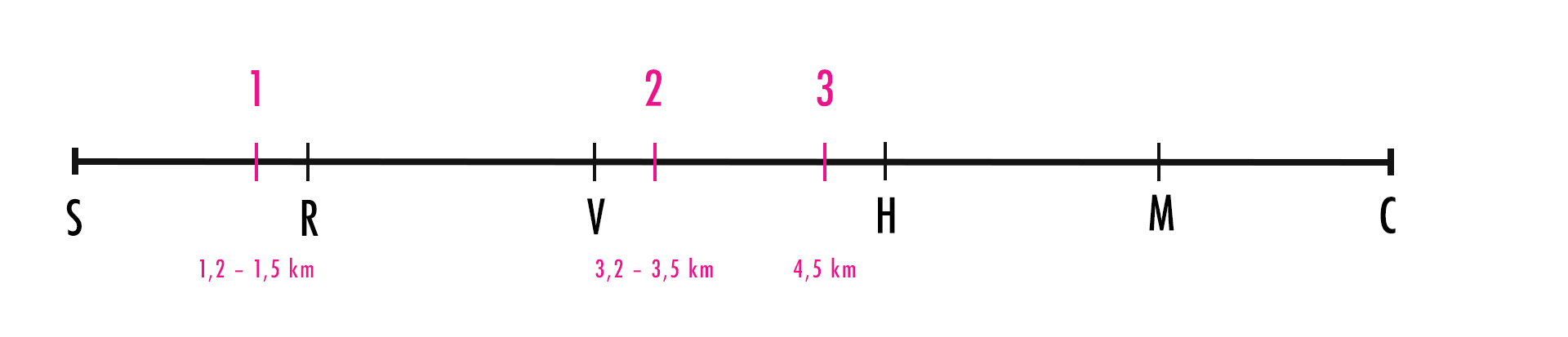
Kontrola 3:

“Kontrola 3 je v troch štvrtinách trasy”

Jednoducho vyrátame tri štvrtiny zo 6 km:

1/4 z 6 = 1,5

3/4 z 6 = 1,5*3 = 4,5 km

Tentokrát dostávame presný údaj a vieme s istotou, že kontrola 3 sa nachádza na 4,5 km. Bod H je až na 4,8 km, nachádzame sa teda stále ešte medzi bodmi V a H:

Kontrola 4:

“ku kontrole 4 je to z nej menej ako šestinu dĺžky závodu. Z kontroly 4 zostáva už menej ako osmina trasy do cieľa”.

Najskôr sa zameriame na prvú vetu. Tá nám hovorí, že z kontroly 3 je to ku kontrole 4 menej ako šestina dĺžky závodu:

1/6 z 6 = 1 km

4,5 km + 1 km = 5,5 km

Vieme teda, že kontrola 4 je určite pred 5,5 km, čo je zhodou okolností aj presná pozícia bodu M. Z tohto dôvodu môžeme odvodiť, že kontrola 4 sa určite nachádza pred týmto bodom.

Je nám teda k niečomu nasledujúca veta? Potrebujeme k niečomu vedieť, že z kontroly 4 zostáva menej ako osmina trasy do cieľa? Samozrejme, pretože sme síce umiestnili kontrolu 4 pred M, ale musíme sa uistiť, či sa náhodou nemôže aj táto štvrtá kontrola nachádzať ešte pred bodom H.

1/8 z 6 = 0,75

6 - 0,75 = 5,25 km

Odčítali sme osminu trasy a tým sme dostali hodnotu, za ktorou musí ležať kontrola 4. Vieme teda, že to musí byť nie pred 5,5 km a zároveň až za 5,25 km. Môžeme teda s istotou povedať, že kontrola 4 leží medzi bodmi H a M:

Toto je výsledná podoba našej osi, v ktorej máme zanesené všetky údaje, ktoré sme zo zadania mohli vyčítať. Teraz si prejdeme možnosti a zhodnotíme, ktorá z nich nám s osou neladí:

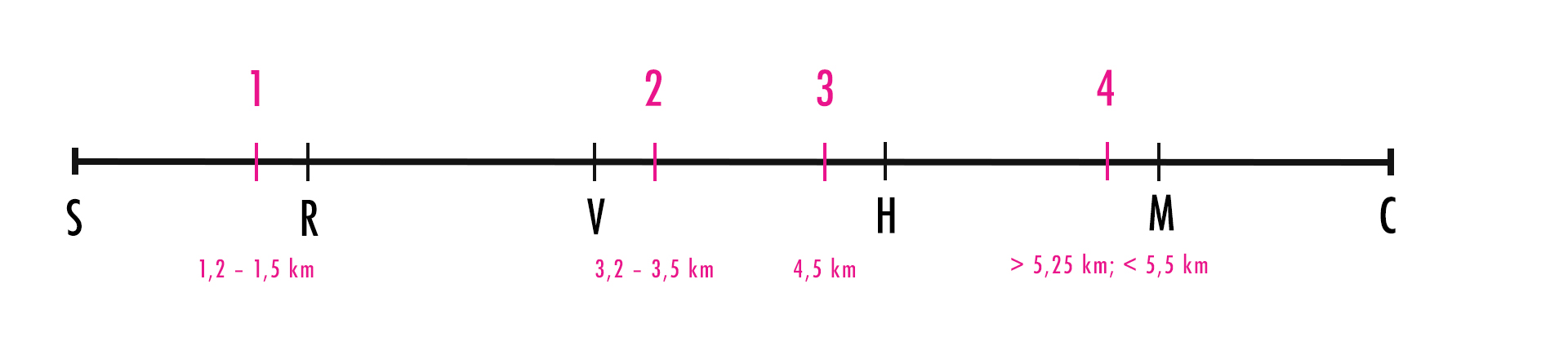
Medzi vrcholom V a hotelom H sú dve kontroly.

Kontrola 2 je za vrcholom V.

Medzi rybníkom R a vrcholom V je jedna kontrola. - Táto možnosť nesedí s osou, medzi R a V sa nenachádza žiadna kontrola, preto je táto odpoveď nesprávna.

Medzi mostom M a cieľom C nie je žiadna kontrola.

Kontrola 4 je pred mostom M.